|
Cerchio di confusione e profondità di campo
Nella ipotesi di obiettivo ideale, cioè in grado di mettere a fuoco una immagine senza introdurre alcuna deformazione o aberrazione e producendo una immagine estremamente nitida, quale è la risoluzione reale di un sensore? Cioè, quale è la dimensione minima che un sensore riesce a risolvere?
Abbiamo una certezza: sicuramente un sensore non sarà in grado di distinguere particolari dell'immagine di dimensioni inferiori al pixel. Se su un pixel cadono due punti luminosi o uno solo di intensità pari alla somma dei due, il segnale prodotto dal pixel sarà esattamente lo stesso.
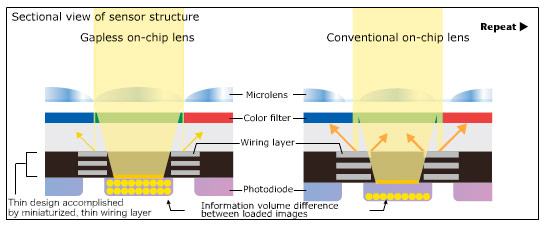
Schematizzazione della dimensione dei singoli pixel in questo esempio mostrato anche nelle variabili di microlenti.
Fonte Nikon raggiungibile anche con animazione tra le pagine Technology del sito Nikon.com.
Facendo crescere le dimensioni dei dettagli, o meglio allontanando tra loro due punti luminosi sul soggetto che producano due punti immagine sul sensore, inizialmente a distanza inferiore alle dimensioni del pixel, ma poi via via a distanza sempre maggiore, si arriverà al punto di notare, nell'immagine digitale prodotta dal sensore, due pixel distinti. Questi due pixel non potranno essere adiacenti, altrimenti non sapremmo mai se i punti del soggetto erano a loro volta adiacenti o distinti ma troppo vicini per essere distinti. Come poteva essere intuitivamente immaginabile servono almeno tre pixel per distinguere due punti. Per distinguere una serie di punti (ad esempio una serie di stanghe parallele di una ringhiera) è necessario che ci siano almeno due pixel per ogni stanga. Nella teoria dei segnali questo limite teorico viene chiamato Teorema del Campionamento di Nyquist citate e descritte anche nella sezione Image Processing Algorithms del sito Nikon: per rappresentare una struttura regolare costituita da N ripetizioni sono necessari almeno 2 volte N pixel.
Ma nella realtà difficilmente raggiungiamo questa definizione e la prima causa è la presenza, davanti al sensore, del filtro anti aliasing. Questo filtro (a volte detto passa basso perché taglia le frequenze spaziali superiori al limite di Nyquist impedendo così il fenomeno dell'aliasing) fa si che in ultima analisi il dettaglio minimo richiede almeno tre pixel per essere catturato e distinto. Ciò che scende al di sotto di tre pixel comincia ad essere confuso, indistinto.
La necessità di questo filtro deriva anche dalla modalità con la quale si generano le tre componenti di colore di un pixel a partire dal Color Filter Array, o matrice di Bayer. La matrice di Bayer determina, nel formato RAW/NEF, la registrazione di una sola componente di colore per ogni pixel, delegando ai pixel adiacenti il compito di fornire le altre due componenti di colore mancanti per arrivare alla modalità RGB. Per avere una adeguata coerenza cromatica nell'ereditare componenti di colore dai pixel adiacenti è necessario che a monte ogni punto dell'immagine venga diffuso (sfocato) anche sui due pixel adiacenti (in orizzontale ed in verticale).
A valle quindi di tutte queste considerazioni possiamo ragionevolmente definire una areola di tre pixel di diametro al di sotto della quale i dettagli non sono più distinguibili in modo netto. Chiamiamo questa areola cerchio di confusione.
Se non consideriamo l'obiettivo come un oggetto ideale, allora va tenuto conto anche della nitidezza ed incisione dell'obiettivo stesso. La misura della nitidezza di un obiettivo, in genere espressa con la Modulation Transfer Function “MTF”, esula dai confini di questo articolo, e quindi non viene qua presa in considerazione, ma è importante ricordare che la profondità di campo è tanto maggiore quanto “peggiore” è la MTF.
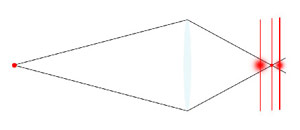
Dalla Fig 8 che riportiamo nuovamente si vede che allontanandosi dal piano focale l'obiettivo produce un punto dell'immagine sempre più sfocato e più largo, ma fino a quando le dimensioni del punto, pur sfocato, rientrano all'interno del cerchio di confusione, non c'è modo di percepire attraverso l'immagine catturata dal sensore se l'immagine stessa è a fuoco o meno.
In altre parole il passo di campionamento spaziale, dell'immagine è maggiore del dettaglio sfocato.
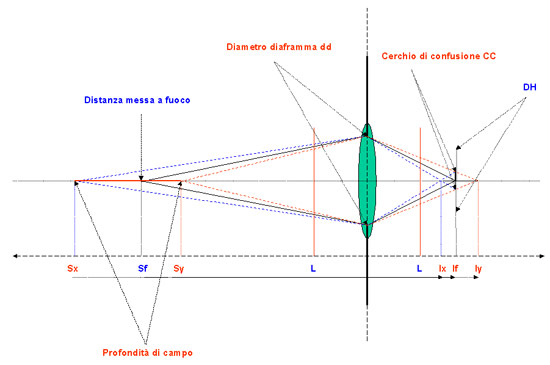
Fig 10: Cerchio di confusione e profondità di campo.
Nella Fig 10 il soggetto principale si trova a distanza Sf dalla lente. Il cerchio di confusione, indicato con CC, è tale che un punto venga percepito con la stessa precisione di messa a fuoco dalla distanza focale Ix fino alla distanza focale Iy. Tra questi due piani il grado di sfocatura dell'immagine rimane sempre inferiore al cerchio di confusione per cui non viene percepito.
Ma alle distanze focali Ix ed Iy, secondo la formula ormai più volte citata, corrispondono, dal lato del soggetto, le distanze Sx ed Sy. Tutto quello che viene posto tra queste due distanze risulterò quindi di nitidezza equivalente a quella di un soggetto alla esatta distanza di messa a fuoco Sf.
Tutto quello che è posto tra la distanza Sx e la distanza Sy apparirà nella immagine con lo stesso grado di messa a fuoco e la distanza tra Sx ed Sy viene detta profondità di campo “PDC”.
Se riduciamo il diaframma, gli angoli formati dalle linee tratteggiate rosse e blu si stringono e continuando a fare passare le linee per i margini del cerchio di confusione otterremo i punti di incrocio (Ix ed Iy) a distanze maggiori rispetto ad If. Corrispondentemente, dalla parte del soggetto, si allontaneranno tra di loro anche i punti Sx ed Sy, incrementando quindi la PDC.
Quando il punto di incrocio Ix arriva alla distanza L dalla lente, ovvero coincide con la lunghezza focale, il corrispondente punto Sx finisce all'infinito. In queste condizioni, cioè nelle condizioni di una PDC che include l'infinito, la distanza Sf viene detta anche distanza iperfocale ed inoltre il punto Sy si troverà a metà tra Sf e la lente.
La PDC dipende quindi da:
-
dimensione del cerchio di confusione (aumenta al crescere del cerchio di confusione)
-
apertura (aumenta con la riduzione del diametro del diaframma)
-
distanza del soggetto (aumenta con la distanza del soggetto)
-
lunghezza focale (aumenta al diminuire della lunghezza focale)
L'ultima dipendenza, quella dalla lunghezza focale, non è così evidente, anzi apparentemente, al diminuire della lunghezza focale gli angoli formati dai raggi che passano per i bordi del diaframma e convergono sul piano focale crescono, e verrebbe spontaneo pensare che “passano di meno” nel cerchio di confusione. In realtà entra in gioco un altro fattore che è quello del rapporto di ingrandimento: minore è la lunghezza focale, minore sarà il rapporto di ingrandimento (If/Sf) e minore sarà la dimensione dell'immagine del soggetto proiettata sul sensore. Senza aggiungere ulteriori formule, basti pensare che al diminuire della lunghezza focale diminuisce anche la dimensione di un dettaglio della scena e di conseguenza diminuisce anche la sua sfocatura in caso di soggetto fuori dal piano di messa a fuoco, facendolo rientrare nella tolleranza di fuoco dovuta la cerchio di confusione. Cosa analoga avviene con il mosso: con una focale corta il mosso si vede molto meno che con una focale lunga.
Foglio di calcolo della profondità di campo
Dagli argomenti sin qui trattati, si evince che la profondità di campo dipende ormai da un numero di parametri che non ne consentono più la stesura sotto forma di tabella, e tanto meno sotto dorma di stampigliatura sull'obiettivo.
D'altra parte il suo calcolo non è immediato e richiede l'applicazione di nozioni di geometria e trigonometria. Esistono nel web diversi siti dove è possibile inserire alcuni parametri ed ottenere la profondità di campo corrispondente. L'Autore ha sviluppato un foglio di calcolo, disponibile su richiesta, che prevede come dati in input (campi in blu):
-
dimensioni del sensore
-
numero di pixel per lato
-
dimensione del cerchio di confusione in pixel
-
lunghezza focale
-
diaframma utilizzato
-
distanza del soggetto
e fornisce i dati calcolati per:
-
dimensioni del pixel
-
numero di megapixel
-
diametro del diaframma
-
superficie aperta del diaframma
-
angolo di campo in gradi
-
dimensioni del cerchio di confusione
-
distanza minima a fuoco
-
distanza massima a fuoco
-
distanza iperfocale
-
distanza minima a fuoco ad iperfocaleg
-
tutti i dati metrici tra lente e sensore
Il foglio è a disposizione di chi ne fa richiesta per e-mail all'autore stesso.
Conclusioni
Questa esplorazione della natura della profondità di campo ci ha dato l'occasione per puntualizzare diversi concetti di ottica geometrica e per descrivere con un certo dettaglio come questi vengono applicati nel caso di sensori digitali.
Il fatto di trovare sul mercato fotocamere reflex con sensori digitali di dimensioni e soprattutto densità di pixel diverse obbliga a rivedere le indicazioni di profondità di campo che una volta erano stampigliate sugli obiettivi. Insieme alla profondità di campo anche altri fattori perdono la loro costanza, come ad esempio l'angolo di campo che non dipende più solo dalla lunghezza focale ma anche dalla dimensione del sensore. Se poi utilizziamo un obiettivo decentrabile in configurazione Jumbo MultiBigShoot, si introduce una ulteriore variabile che è l'escursione del decentramento ottico cui corrisponde un fotogramma finale equivalente ed angolo di campo ottenibile normalmente solo su fotocamere medio formato.
|







