 Introduzione Introduzione
Nel mondo delle reflex il passaggio dalla pellicola al digitale ha segnato una vera e propria rivoluzione, da una parte introducendo concetti estranei al fotografo tradizionale, come workflow, gestione dei dati, formati digitali, tanto per citarne alcuni, dall'altra apportando modifiche a concetti più consueti, come la sensibilità o come la grana, che nel digitale diventa “rumore” e che ha un'origine fisica completamente diversa ma alla fine ha un effetto simile.
La profondità di campo “PDC” è uno dei concetti i cui principi sono rimasti immutati, ma, proprio per la diversità di tecnologia, è diventato più sfuggente e più difficilmente quantificabile.
In questo eXperience ripercorreremo prima i passi principali che portano a definire la PDC, e poi vedremo come la tecnologia digitale, ovvero la sostituzione della pellicola con sensori a diverse risoluzioni, ha portato a dover definire la PDC non solo in base a lunghezza focale e diaframma, come eravamo abituati prima, ma anche in base alle caratteristiche del sensore.
Richiami di ottica geometrica
Per arrivare definire la PDC iniziamo dall'ottica geometrica, ovvero da quella semplificazione dell'ottica che prevede l'uso di lenti sottili che non introducono aberrazioni sferiche significative. In assenza di aberrazioni queste lenti permettono quindi di ottenere da un soggetto una immagine la cui nitidezza è la massima teorica possibile ed è limitata solo dalla lunghezza d'onda della luce utilizzata (messa a fuoco perfetta).
Inoltre non terremo conto della aberrazione cromatica, fenomeno che si verifica in presenza di luce composta da radiazioni a diverse lunghezze d'onda. In pratica la trattazione è valida per una luce monocromatica (tipo laser), ma poi grazie alla linearità del mezzo e per sovrapposizione degli effetti è estensibile a luce bianca come somma di molte radiazioni monocromatiche.
Nel seguito parleremo di lenti o di obiettivi in modo intercambiabile, perché ai fini della descrizione della PDC e della sua misura avere una singola lente oppure gruppi di lenti con un potere ottico equivalente è sostanzialmente la stessa cosa.
CARATTERIZZAZIONE DI UNA LENTE
Una lente si caratterizza attraverso la sua lunghezza focale e la sua apertura relativa.
LUNGHEZZA FOCALE
La lunghezza focale è la distanza focale alla quale viene messa a fuoco l'immagine di un soggetto posto distanza infinita. Se, ad esempio, lasciamo passare la luce del sole attraverso una lente, dal lato opposto l'immagine del sole si metterà a fuoco ad una distanza focale pari alla lunghezza focale.
Nella Fig 1 viene mostrata una lente con lunghezza focale pari a 0.5 (in unità arbitrarie). La lente è nella posizione x=3.
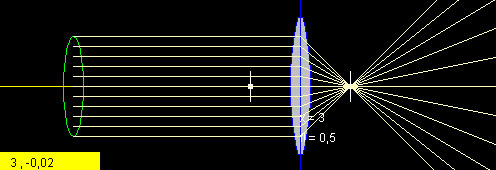
Fig 1: Lunghezza Focale.
Se il soggetto non è posto all'infinito, minore è la sua distanza dalla lente, più lontana dalla lente si formerà la sua immagine. Se Sf è la distanza del soggetto a fuoco e con If indichiamo la distanza alla quale si forma l'immagine oltre la lente, cioè la distanza focale, e con L è la lunghezza focale, vale la formula
1/Sf+1/If = 1/L
che mette in relazione la lunghezza focale L con le distanze del soggetto e della sua immagine dalla lente.
Nelle figure che seguono la lente ha sempre lunghezza focale L=0,5 (unità arbitrarie) ed il centro della lente è ad x=3.
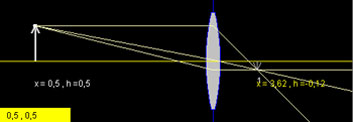
In Fig 2 il soggetto è ad x=0.5 quindi a distanza Sf=2.5 dalla lente. Secondo la formula avremo If = 1/(1/L-1/Sf) = 0.62. Quindi l'immagine del soggetto si forma ad una distanza focale If=0.62, cioè sul piano focale posto ad x=3.62.
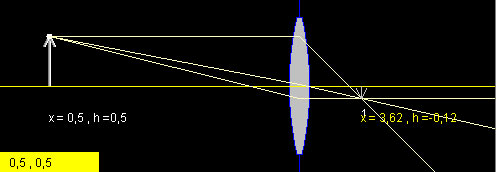
Fig 2: Distanza soggetto lontano e distanza focale.
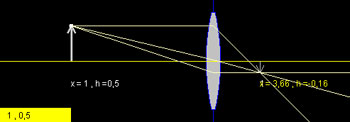
Nella figura Fig 3 il soggetto è più vicino alla lente (x=1 cioè Sf=2). Applicando la formula si trova che If= 0.66 e l'immagine si forma ad x=3.66, a distanza quindi superiore rispetto a prima.
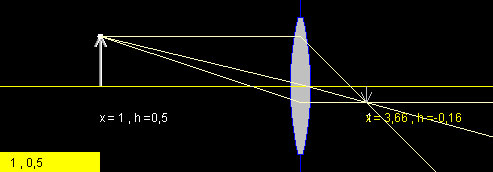
Fig 3: Distanza soggetto vicino e distanza focale.
In teoria la distanza minima alla quale può arrivare il soggetto rispetto alla lente e che permette il formarsi di una immagine, è proprio la lunghezza focale, ma questo comporterebbe una immagine formata proiettata all'infinito. Nella pratica la distanza minima di messa a fuoco è dettata dalla escursione massima della lente rispetto al sensore. Più la lente può allontanarsi dal sensore (maggiore è If) più vicino può stare il soggetto (minore è Sf).
APERTURA RELATIVA
L'altro parametro che caratterizza una lente, o un obiettivo con il suo completo schema ottico ed il suo diaframma, è l'apertura relativa, anche espressa con il simbolo f/, che rappresenta il rapporto tra la lunghezza focale ed il diametro del diaframma.
f/ = L / DD
con L = lunghezza focale e DD = diametro del diaframma.
Ugualmente si può scrivere:
DD = L / f/
Un obiettivo, ad esempio, con lunghezza focale 105mm, e con una apertura relativa impostata su f/2.8 presenterà un diaframma di 105/2.8 = 37.5mm di diametro.
Vale la pena ricordare la progressione dei valori standard di apertura relativa:
f/1, f/1.4, f/2, f/2.8, f/4, f/5.6, f/8, f/11, f/16, f/22, f/32, f/44, f/64
dove f/1 rappresenta l'apertura relativa più luminosa.
I valori di questa scala sono distanziati di 1 stop, ovvero di quella differenza di esposizione che corrisponde ad un raddoppio del flusso di luce (+1 stop) o ad una riduzione alla metà del flusso di luce (-1 stop).
Se ad esempio prendiamo un obiettivo con lunghezza focale di 50mm, dall'apertura relativa possiamo ricavare il diametro del diaframma:
DD = 50mm / f/
La metà del diametro corrisponde al raggio Ra dal quale possiamo calcolare l'area del diaframma, cioè la superficie attraverso la quale il diaframma fa passare la luce
Area = Ra2 x 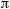 ( ( 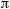 = pi greco = 3,1415....) = pi greco = 3,1415....)
|
Obiettivo con lunghezza focale di 50 mm
|
|
f/2 |
diametro = 25.00mm |
area = 490.6 mm2 |
|
f/2.8 |
diametro = 17.85mm |
area = 250.3 mm2 |
|
f/4 |
diametro = 12.50mm |
area = 122.6 mm2 |
|
f/5.6 |
diametro = 8.92mm |
area = 62.5 mm2 |
Si vede quindi come la progressione delle aperture relative corrisponda ad aree che ad ogni passo si dimezzano riducendo quindi di uno stop l'esposizione (“passa” la metà della luce).
APERTURA RELATIVA EFFETTIVA
L'apertura relativa stampigliata sul corpo dell'obiettivo è quella nominale, ovvero è l'apertura relativa che l'obiettivo presenta quando la messa a fuoco è all'infinito e la distanza focale coincide con la lunghezza focale.
Ma abbiamo visto che all'avvicinarsi del soggetto il piano focale sul quale si forma la sua immagine si allontana dalla lente, cioè la distanza focale Df aumenta. Questo ha una conseguenza sulla luminosità perché, a parità di diametro del diaframma (DD) il rapporto distanza focale/diametro del diaframma cambia, aumentando (ovvero muovendosi verso aperture relative con numero maggiore, quindi con minore luminosità).
L'apertura relativa effettiva fe/ si può calcolare partendo dalla distanza focale If e dal diametro del diaframma DD:
fe/ = If/DD
oppure dall'apertura nominale f/ e dal rapporto di ingrandimento (di seguito definito):
fe/ = (1+1/R)*f/
RAPPORTO DI INGRANDIMENTO
Dagli schemi molto semplici delle Fig 2 e Fig 3 già visti in precedenza, possiamo ricavare anche un altro importante parametro legato alla lunghezza focale ed alla distanza del soggetto: il rapporto di ingrandimento R.
Questo è il rapporto tra dimensione dell'immagine HI e la dimensione del soggetto HS:
R = HI/HS
Nelle figure l'altezza del soggetto è sempre h=0.5, invece l'altezza della sua immagine cambia ed aumenta all'avvicinarsi del soggetto alla lente.
Il rapporto tra le due altezze HI/HS, cioè il rapporto di ingrandimento R, risulta essere uguale al rapporto tra la distanza focale e la distanza del soggetto a fuoco, cioè
R = If/Sf
Facciamo un esempio: fotografiamo un oggetto alto un metro (HS = 1000 mm) alla distanza di 5 metri (Sf = 5000 mm) con un obiettivo con lunghezza focale L=100 mm.
Per prima cosa possiamo calcolare If attraverso la formula già usata:
If = 1/(1/100 – 1/5000)
ed otteniamo If=102 mm. Questo vuol dire che l'immagine del soggetto verrà a fuoco su un piano a 102 mm dalla lente (oppure a 2 mm oltre la sua lunghezza focale). Il rapporto di ingrandimento sarà quindi R = If/Sf = 0.0204 ovvero circa 1/50. L'immagine del soggetto sul sensore sarà quindi grande HI = 1000/50 = 20 mm.
|







